When to get married (using Python)
Inspiration for this comes from Dr. Hannah Fry’s Ted Talk on the mathematics of love. Part of the talk centers on using optimal stopping theory to answer the popular question: “When is it time to stop dating and settle down?” Let’s try to answer this using simulation (there’s already a proven mathematical answer, this is just for fun).
Setup
Suppose over the course of your dating life, you could potentially have a maximum of 20 romantic partners. We’ll assign each person you date with a compatability score from 1 to 100 (no negatives - I assume if you’re going on a date with someone, you have to be sort of into them). The rules: you can only choose to marry or dump your current partner. You cannot look into the future and see potential partners and once you are married, you exit the rat race and stop dating for good.
The strategy for picking the optimal partner probably isn’t marrying the first person you date, nor is it waiting until your last dating partner. The “best” strategy is something along the lines of outright rejecting the first $X$% of people you date in order to gather a sample of data, then marrying the first person who comes along who is better than anyone you have dated before. Of course, you run the risk of rejecting your true love outrightly, but we’re looking for the best overall strategy here. The goal of this simulation is finding the best initial percentage of people to reject i.e. when is it best to “stop screwing around” (not my words).
We’ll compare different stopping times by simulating thousands of sequences of dating partners and comparing the compatability scores of the chosen married partners.
The coding bit
Generating a sequence of partners is easy enough using numpy:
import numpy as np
np.random.seed(182)
partners = np.random.randint(low = 1, high = 100, size = 20)The “toughest” part for us is writing a function that will implement whatever cutoff rule we choose and return the score of the partner we marry.
Thankfully it’s not too tough.
Here we assign the input cutoff_point to be the index for the last partner which we will outright reject (19 would imply we marry the last person we date and 0 would imply that we marry the first person we date).
def get_married(partners, cutoff_point):
if cutoff_point not in range(0,len(partners)):
print("invalid stopping point provided. must be between 0 and 19.")
return
elif cutoff_point == 0:
return partners[0]
else:
max_previous_partners = np.max(partners[0:cutoff_point])
partners_left = partners[cutoff_point:len(partners)]
n_partners_left = len(partners_left)
for i in range(0, n_partners_left):
if i == (n_partners_left - 1):
return partners[len(partners) - 1]
else:
partner = partners_left[i]
if partner > max_previous_partners:
return(partner)I’m not an expert Python programmer, but this function gets the job done.
Results
Let’s generate 10000 independent dating lives and see how each of the cutoff rules perform using the mean compatability score of the people we marry! Here’s a quick snippet that will do it for us:
try_cutoff = range(0, 20)
n_sims = 10000
results = [None]*n_sims
for cutoff in try_cutoff:
for j in range(len(results)):
partners = np.random.randint(low = 1, high = 100, size = 20)
results[j] = get_married(partners, cutoff)
print("for cutoff {} the average score was {}.".format(cutoff, np.mean(results)))We can plot these mean compatability scores with the different cutoff points on the x-axis.
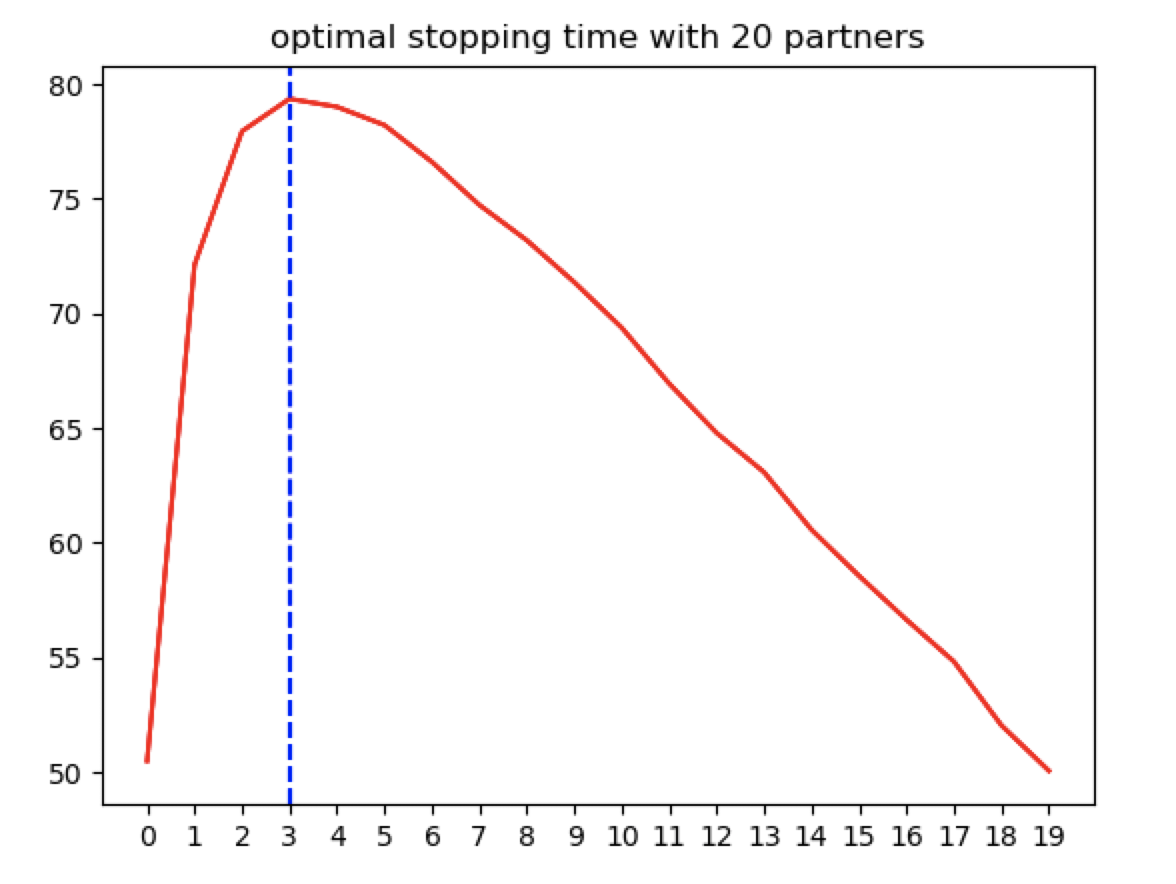
According to our results, if you are expecting to date 20 people in your lifetime, rejecting the first 4 people you meet and marrying the first person to come along afterwards who is better than anyone you dated before is on average the best strategy!
Wait… huh?
According to all available resources on this problem, the optimal cutoff should be the first ~37% of the search space. In our scenario, this would mean rejecting the first 7 or 8 people! What gives?
In this scenario, we have fixed the number of available dating partners to 20. It simply seemed like a reasonable number. On average though across all possible numbers of partners, the best rule should be around 37%.